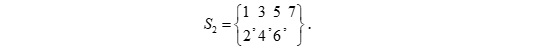У сучасному світі, де обчислювальні вимоги постійно зростають, а можливості послідовної обробки даних обмежені, паралельні алгоритми відіграють ключову роль. Вони дають змогу суттєво збільшити швидкість обчислень завдяки одночасному виконанню операцій над різними фрагментами інформації чи частинами завдання. Застосування паралельних обчислень дозволяє максимально ефективно використовувати апаратні можливості сучасних систем, що прискорює розв’язання складних задач, які у традиційному послідовному підході вимагали б значно більше часу та ресурсів.
Процес побудови паралельної форми алгоритму передбачає побудову орграфів залежностей, які визначають оптимальний порядок виконання операцій [1]. Нехай граф G = (V, U) – зв’язний ациклічний орієнтований граф, де вершинам відповідають обчислювальні операції алгоритму |V| = n, а елементи множини U задають порядок виконання операцій. Дуга (i, j) належить графу тоді коли операція i безпосередньо передує операції j.
Тоді існує таке число H < n, що кожну з вершин графа можна позначити одним з індексів від 0 до H, таким чином що якщо дуга виходить з вершини з індексом a та входить у вершину з індексом b, то a < b. Група вершин, що мають однакові індекси називаються ярусом паралельної форми, а кількість вершин у ярусі — шириною ярусу. Кількість ярусів у паралельній формі (крім нульового ярусу) називається висотою паралельної форми, яка рівна числу H, а шириною — максимальне значення ширини ярусів. Основною метою задачі побудови паралельної форми алгоритму є мінімізація висоти паралельної форми при заданій ширині або мінімізація ширини, при заданій висоті. Тобто в основі побудови ефективної паралельної форми алгоритму фактично лежить пошук відповідного графу.
Розглянемо побудову паралельної форми знаходження суми елементів 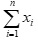 . Застосувавши каскадну схему можна розпаралелити порядок виконання операцій. На рис. 1 зображено паралельну форму такого алгоритму для восьми вхідних елементів, які знаходяться на нульовому ярусі. Вершинам, що відповідають виконанню операцій поставлені у відповідність номери від 1 до 7.
Рисунок 1 - Орграф каскадної схеми суми восьми вхідних елементів
Ширина каскадної схеми для n вхідних елементів складає 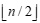 , а висота 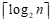 . Цілком зрозуміло, що оскільки між вхідними даними не існує обмежень на порядок слідування операцій, то на першому ярусі кількість можливих варіантів сум елементів може бути C n2. Аналогічно буде визначатися кількість можливих варіантів і на ярусах паралельної форми, до передостаннього включно. Слід зазначити, що при розв'язанні деяких практичних задач, в яких початкові дані мають велику розмірність, кінцеві результати отримані за різними формами можуть відрізнятися внаслідок округлення.
Паралельним упорядкуванням S вершин орграфа G називається таке їх розміщення на місцях, що розташовані в лінію, при якому на кожному місці стоїть хоча б одна вершина, причому якщо то вершина i розміщена раніше вершини j [2]. Довжиною упорядкування l(S) називають кількість непорожніх місць в S, а шириною h(S) величину max|S[k]|, де S[k] - множина вершин, що стоять в S на місці k.
На відміну від задач побудови паралельних форм, у задачах упорядкування структура графу є фіксованою. Залежно від постановки задачі оптимізація виконується шляхом пошуку упорядкування мінімальної довжини (аналог висоти паралельної форми) при заданій ширині або мінімальної ширини (аналог ширини паралельної форми) при заданій довжині.
Для зображеного на рис. 1 графу виконання операцій каскадної схеми можна побудувати упорядкування:
Таке упорядкування має фіксовану ширину h = 2 та довжину l = 5. Але наведене упорядкування не є оптимальним. Якщо змінити порядок виконання операцій, то можна отримати упорядкування меншої довжини для тієї самої ширини:
Отримане упорядкування є оптимальним. Оскільки для графів, що мають структуру вхідних дерев, відомий точний алгоритм поліноміальної складності побудови оптимальних паралельних упорядкувань, то відповідні паралельні форми алгоритмів можуть бути знайдені на основі оптимальних упорядкувань.
Введення додаткових обмежень у задачах упорядкування, при яких можливий рівномірний розподіл вершин, дозволить будувати ефективні паралельні форми алгоритмів.
Список літератури
1. Коцовський В. М. Теорія паралельних обчислень : навч. посіб. Ужгород : ПП «АУТДОР-Шарк», 2021. 188 с.
2. Турчина В. А., Федоренко Н. К. Використання орграфів при моделюванні паралельних процесів. Матеріали 11-го Міжнародного науково-практичного семінару «Комбінаторні конфігурації та їх застосування». Кіровоград 2011. С. 178-181.
|








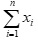 . Застосувавши каскадну схему можна розпаралелити порядок виконання операцій. На рис. 1 зображено паралельну форму такого алгоритму для восьми вхідних елементів, які знаходяться на нульовому ярусі. Вершинам, що відповідають виконанню операцій поставлені у відповідність номери від 1 до 7.
. Застосувавши каскадну схему можна розпаралелити порядок виконання операцій. На рис. 1 зображено паралельну форму такого алгоритму для восьми вхідних елементів, які знаходяться на нульовому ярусі. Вершинам, що відповідають виконанню операцій поставлені у відповідність номери від 1 до 7.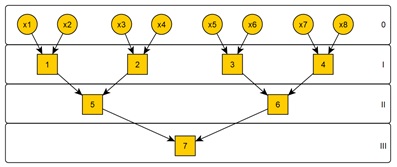
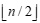 , а висота
, а висота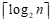 . Цілком зрозуміло, що оскільки між вхідними даними не існує обмежень на порядок слідування операцій, то на першому ярусі кількість можливих варіантів сум елементів може бути Cn2. Аналогічно буде визначатися кількість можливих варіантів і на ярусах паралельної форми, до передостаннього включно. Слід зазначити, що при розв'язанні деяких практичних задач, в яких початкові дані мають велику розмірність, кінцеві результати отримані за різними формами можуть відрізнятися внаслідок округлення.
. Цілком зрозуміло, що оскільки між вхідними даними не існує обмежень на порядок слідування операцій, то на першому ярусі кількість можливих варіантів сум елементів може бути Cn2. Аналогічно буде визначатися кількість можливих варіантів і на ярусах паралельної форми, до передостаннього включно. Слід зазначити, що при розв'язанні деяких практичних задач, в яких початкові дані мають велику розмірність, кінцеві результати отримані за різними формами можуть відрізнятися внаслідок округлення.