Існує ряд прикладних задач, в яких або при певній кількості ресурсів, що виділена на виконання скінченної множини завдань, на порядок виконання яких накладені певні технологічні обмеження, потрібно використати ресурси так, аби завершити завдання за мінімальний час; або при заданому терміні завершення мінімізувати кількість ресурсів для виконання таких завдань. Такі задачі виникають у будівництві, автомобілебудуванні, при розпаралеленні обчислень та в багатьох інших сферах. Їх можна звести до оптимізаційних задач на графах.
Розглянемо задачі, які можна розглядати як задачі впорядкування певної множини елементів. Серед них виділимо підклас, в яких задані скінченна множина завдань, які потрібно виконати; технологічні обмеження на порядок їх виконання; та час завершення виконання завдань або скінченна множина ресурсів для їх виконання. На основі цього в [1] сформульовані наступні задачі.
Задача 1. Потрібно визначити розподіл завдань по взаємно замінних ресурсах так, аби завдання виконались за мінімальний час без порушення технологічних обмежень.
Задача 2. Розподілити завдання у певному часовому діапазоні так, щоб було використано мінімальну кількість ресурсів без порушення технологічних обмежень.
Наведемо математичні постановки цих задач. Нехай множина завдань містить n елементів, і вважаємо, що елементи цієї множини – натуральні числа від 1 до n. Обмеження на порядок виконання можна подати у вигляді орієнтованого графу G = (V, U), де V – множина вершин, ǀVǀ=n, U – множина дуг, (i,j)ϵ U, якщо завдання з номером i безпосередньо йде перед завданням з номером j. Розподіл завдань можна подати у вигляді паралельного упорядкування S вершин графу G. Час можна подати як довжину упорядкування l, а кількість ресурсів – як ширину h.
Задача 1. Задано граф G та ширину упорядкування. Потрібно побудувати паралельне упорядкування, довжина якого буде мінімальною.
Задача 2. Задано граф G та довжину упорядкування. Потрібно побудувати паралельне упорядкування, ширина якого буде мінімальною.
Розглянемо задачу 2, коли задана довжина упорядкування дорівнює довжині критичного шляху графу. У цьому випадку місця вершин, що лежать на критичних шляхах, визначаються однозначно. Решта вершин матимуть діапазон можливого розміщення.
Цю задачу можна звести до задачі про максимальний умовний потік. Для цього вводиться спеціальна (s, t)-мережа, в основі якої – дводольний граф. Будується вона наступним чином.
У першу (ліву) долю заносимо вершини початкового графа, у другу (праву) долю – вершини, що відповідатимуть місцям в упорядкуванні, що будується. Вводимо джерело, з якого у кожну вершину лівої долі проводимо по одній дузі з пропускною здатністю 1. Також вводимо стік, в який з кожної вершини правої долі проводимо по одній дузі з пропускною здатністю h, значення якої потрібно попередньо оцінити.
Дуги, що з’єднують вершини лівої та правої долей, будуються на основі діапазонів допустимих місць вершин. З вершин першої долі виходять дуги у вершини другої долі, що відповідають місцям у діапазоні розміщення. З вершин, що лежать у початковому графі на критичних шляхах, буде виходити лише одна дуга у вершину правої долі. Пропускна здатність всіх дуг, що з’єднують ліву та праву долі, дорівнює 1.
Після побудови мережі можна знайти максимальний потік алгоритмом Форда-Фалкерсона та побудувати на його основі наближений розв’язок. Якщо не вдалося побудувати максимальний потік величини n, то потрібно збільшити величину h на одиницю, і, як наслідок, пропускну здатність дуг, що йдуть з правої долі в стік і продовжити цю процедуру доти, доки не буде побудовано максимальний потік величини n.
Розглянемо задачу 1, коли задана ширина упорядкування. Її також можна звести до задачі про максимальний умовний потік. Для цієї задачі (s, t)-мережа будується аналогічно до попереднього випадку, але потрібно оцінити попередньо довжину l. Якщо не вдасться побудувати максимальний потік величини n, то потрібно збільшити величину l на одиницю, і, як наслідок, додати у праву долю одну вершину.
Проте, якщо було отримано максимальний потік величини n, то в обох задачах це не гарантує того, що отриманий розв’язок буде допустимим, оскільки можуть бути порушені технологічні обмеження на порядок виконання. У цьому випадку потік потрібно змінити. На цьому етапі починає працювати схема направленого перебору, а отже, час зростає експоненційно.
Розглянемо одне із узагальнень задачі 1.
Задано граф G = (V, U) та задані обмеження на потужність множини S[i] у вигляді вектору 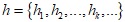 , які означають, що на і-му місці може бути не більше вершин.
У цій задачі не вдається апріорі оцінити знизу довжину упорядкування. Тому це питання потребує подальших досліджень і доти, доки не буде отримана оцінка, звести цю задачу до задачі про максимальний умовний потік неможливо. Крім того, потребують досліджень і питання існування щільних упорядкувань для неї, аналогічні результатам, отриманим в [2].
Список літератури:
1. Coffman E.G., Bruno J. Computer and job-shop scheduling theory. New York : Wiley, 1976. 299 p.
2. Turchyna V., Karavaiev K. Analysis of algorithms for constructing dense sequencing of digraphs vertices. Proceedings of The Third International Workshop on Computer Modeling and Intelligent Systems (CMIS-2020), Zaporizhzhia, 2020. P. 690–703. URL: https://ceur-ws.org/Vol-2608/paper53.pdf (дата звернення 21.03.2025).
_____________________
Науковий керівник: Турчина Валентина Андріївна, кандидат фізико-математичних наук, доцент, Дніпровський національний університет імені Олеся Гончара
|








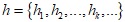 , які означають, що на і-му місці може бути не більше вершин.
, які означають, що на і-му місці може бути не більше вершин.