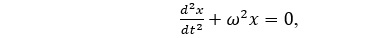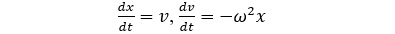Python є однією з найпопулярніших мов програмування для вирішення фізичних задач завдяки своїй простоті, універсальності та широкому вибору наукових бібліотек. Її зрозумілий синтаксис дозволяє легко писати та читати код, що робить Python доступним навіть для початківців у програмуванні. Однією з ключових переваг Python є наявність потужних бібліотек для числових обчислень і моделювання, таких як NumPy, SciPy та SymPy. Вони дозволяють швидко виконувати операції з масивами даних, розв’язувати рівняння, інтегрувати та оптимізувати фізичні моделі.
Крім того, Python забезпечує ефективну візуалізацію результатів завдяки бібліотекам Matplotlib і Plotly, які дозволяють створювати графіки, діаграми та анімації для аналізу фізичних явищ. Для моделювання динамічних систем і розв’язання диференціальних рівнянь Python пропонує спеціалізовані інструменти, зокрема в межах SciPy. Завдяки бібліотекам, таким як VPython, фізики можуть візуалізувати процеси у 3D або створювати інтерактивні симуляції.
Python також підтримує символьні обчислення за допомогою бібліотеки SymPy, що корисно для розв’язання складних математичних задач, таких як спрощення виразів, символьне диференціювання та інтегрування. У фізиці часто виникає необхідність роботи з великими обсягами даних, і Python пропонує зручні інструменти для їх обробки, аналізу та збереження, такі як Pandas.
Мова дозволяє інтегрувати код із програмами на C, C++ та Fortran, що особливо актуально для оптимізації обчислень у складних моделях. Додатково, Python підтримує паралельні обчислення, що важливо для задач, пов’язаних із моделюванням фізичних процесів чи обробкою великих даних. У галузях, таких як квантова механіка, надпровідність та астрофізика, Python також пропонує спеціалізовані бібліотеки, наприклад QuTiP і Astropy.
Python є універсальним інструментом для моделювання фізичних систем, розв’язання задач теоретичної фізики та аналізу експериментальних даних. Його можливості інтеграції з лабораторним обладнанням, а також створення інтерактивних середовищ, таких як Jupyter Notebook, роблять Python незамінним для сучасних фізиків як у наукових дослідженнях, так і в освітньому процесі.
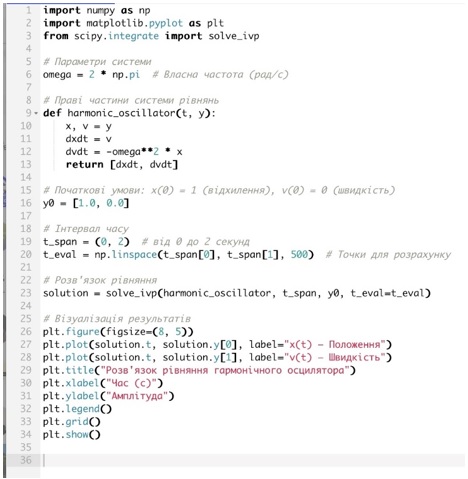
Для ілюстрації використання Python у фізичних задачах розглянемо розв’язок звичайного диференціального рівняння (ODE), яке описує фізичний процес. Наприклад, рівняння гармонічного осцилятора:
де x(t) – положення осцилятора в момент часу t, а ω - власна частота.
Це рівняння можна переписати у вигляді системи першого порядку:
Для розв’язання цієї системи в Python можна скористатися функцією solve_ivp з бібліотеки scipy.
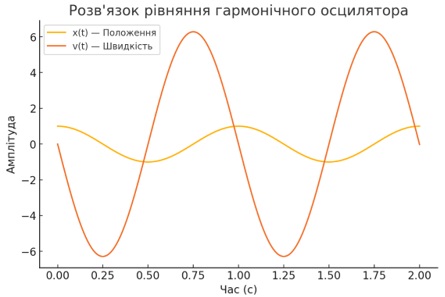
Рис. 1. гармонічні коливання, де: x(t) (положення) змінюється синусоїдально, відображаючи амплітуду осциляцій; v(t) (швидкість) зміщується по фазі на π/2 відносно x(t), як очікується для гармонічного осцилятора.
Отже, на графіку видно гармонічні коливання, де x(t) і v(t) змінюються синусоїдально, як очікується для гармонічного осцилятора. Такий підхід можна легко адаптувати до інших фізичних систем, наприклад, демпфованого осцилятора, маятника або систем із зовнішньою силою.
Література
1. Alexander Koryagin, Roman Khudorozkov, Sergey Tsimfer PyDEns Python Framework for Solving Differential Equations with Neural Networks Machine Learning 2019.
|
Голосування 
Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License
Знайшли помилку? Виділіть помилковий текст мишкою і натисніть Ctrl + Enter