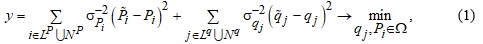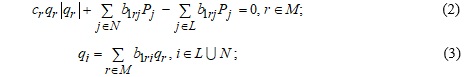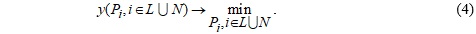У даній роботі розглядається математична постановка задачі оцінювання стану моделі сталого потокорозподілу (СПР) інженерної мережі (ІМ) і пропонується ефективний метод її розв’язання.
Задача оцінювання стану моделі СПР полягає в оцінюванні режимних параметрів, що описують повний потокорозподіл ІМ, на підставі вимірювання лише деяких з них. Основою для формулювання задачі оцінювання стану є модель СПР [1, с. 169].
Розглянемо математичну постановку задачі оцінювання стану моделі СПР в ІМ. Розглядається ІМ, структура якої задається у вигляді графа G(V,E), що містить e=Card(E) дуг і v=Card(V) вершин. Множину E дуг графа мережі можна представити як E=M U K, де M – множина дуг графа мережі, що відповідають реальним ділянкам; K=L U N – множина фіктивних ділянок мережі; L – множина дуг, що відповідають входам мережі; N – множина дуг, що відповідають виходам мережі.
Відомі параметри реальних ділянок мережі ci,i є M, а також виміряні значення тиску  і витрат 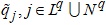 , де LP, NP – множини фіктивних дуг, що відповідають входам і виходам мережі, де проводилося вимірювання тиску; Lq, Nq – множини фіктивних дуг, що відповідають входам і виходам мережі, де проводилися вимірювання витрат. Відомі також дисперсії виміряних величин тиску σ2Pi, iϵLP U NP і витрат σ2qj, jϵLq U Nq. Кількість вимірювань перевищує сумарну кількість входів і виходів ІМ. Виконання даної умови відповідає виконанню умов топологічної ідентифікованості ІМ.
Потрібно отримати оцінки дійсних значень вимірюваного тиску Pi, i ϵ LP U NP і витрат qj, j ϵ Lq U Nq, а також всіх функціонально пов'язаних з ними змінних qi,iϵM U L U N; Pj,jϵL U N, що характеризують потокорозподіл в ІМ, тобто оцінити всі компоненти вектора стану.
Для побудови процедури оцінювання використовуватимемо метод максимальної правдоподібності, згідно з яким формальна постанова задачі матиме вигляд [2, с. 51]:
де Ω – область, що визначається рівняннями моделі СПР.
Таким чином, формальна постановка задачі оцінювання стану моделі СПР приводить до задачі умовної оптимізації.
Вибір методу розв’язання задачі (1) істотно залежить від конкретного представлення рівнянь моделі СПР.
Підвищення ефективності розв’язання задачі оцінювання стану моделі СПР може бути досягнуте за рахунок використання топологічних властивостей графа мережі і способу вибору незалежних змінних.
Пропонується область Ω описувати системою рівнянь моделі СПР такого вигляду:
де Pj – тиск на початку (jϵN) або кінці (jϵL) j- ої фіктивної дуги; b1ri– елемент цикломатичної матриці B1, побудованої для гілок дерева графа мережі; qi – витрата по i - ій ділянці мережі.
Отже, задача оцінювання стану моделі СПР є задачею мінімізації функції (1) при обмеженнях (2), (3).
Система рівнянь (2), (3) є системою m+l+n рівнянь відносно m+2l+2n змінних qi,iϵM U L U N і Pj,jϵL U N. Розділимо змінні задачі на залежні і незалежні. До незалежних змінних віднесемо тиск в дугах, що відповідають входам і виходам мережі Pj,jϵL U N, до залежних – витрати qi,iϵM U L U N.
Тоді задача умовної мінімізації з нелінійними обмеженнями зводиться до задачі безумовної мінімізації тільки відносно незалежних змінних:
Для розв’язання задачі (4) доцільно використовувати модифікації методів оптимізації другого порядку, що дозволяють .розв’язувати задачу мінімізації багатоекстремальних функцій, зокрема, узагальнений метод Ньютона з приведенням матриці Гессе до діагонального вигляду. Даний метод дозволяє встановити напрям зменшення цільової функції, якщо поточне наближення знаходиться в околі або безпосередньо в точці максимуму чи в сідловій точці.
Список літератури
1. Козиренко С. І., Ільницький В.Б. Ідентифікація стану моделі сталого потокорозподілу у інженерних мережах // Інноваційні технології в науці та освіті. Європейський досвід: матеріали V міжнародної конференції, 29 листопада 2022 р. Дніпро, 2022. С 169-172.
2. Евдокимов А.Г., Тевяшев А.Д. Оперативное управление потокораспределением в инженерных сетях. - Харьков: Вища школа, 1980. - 144c.
|








 і витрат
і витрат 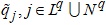 , де LP, NP – множини фіктивних дуг, що відповідають входам і виходам мережі, де проводилося вимірювання тиску; Lq, Nq – множини фіктивних дуг, що відповідають входам і виходам мережі, де проводилися вимірювання витрат. Відомі також дисперсії виміряних величин тиску
, де LP, NP – множини фіктивних дуг, що відповідають входам і виходам мережі, де проводилося вимірювання тиску; Lq, Nq – множини фіктивних дуг, що відповідають входам і виходам мережі, де проводилися вимірювання витрат. Відомі також дисперсії виміряних величин тиску