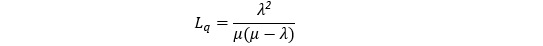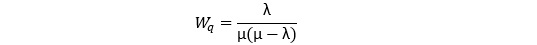Системи масового обслуговування (СМО) відіграють ключову роль у сучасному світі, де ефективне управління ресурсами та оптимізація процесів стають все більш критичними. Ці системи, що базуються на теорії черг, знаходять широке застосування в різноманітних галузях - від телекомунікацій до охорони здоров'я, від виробництва до інформаційних технологій [1, с. 42]. СМО представляють собою комплексні структури, призначені для обробки потоку запитів або клієнтів, що надходять, з метою забезпечення ефективного обслуговування при оптимальному використанні наявних ресурсів.
У контексті інформаційних технологій та сучасних сервісних архітектур, системи масового обслуговування набувають особливого значення. Вони лежать в основі проектування та реалізації високонавантажених систем, здатних обробляти величезні обсяги запитів у реальному часі. Це особливо актуально для компаній, які надають API-сервіси, зокрема у сфері штучного інтелекту, хмарних обчислень та SaaS-рішень.
Теорія черг, яка є фундаментом СМО, дозволяє моделювати поведінку системи в умовах змінного навантаження та оптимізувати її параметри для досягнення бажаного балансу між якістю обслуговування та ефективністю використання ресурсів. Основні компоненти СМО включають вхідний потік запитів, чергу, обслуговуючі пристрої та вихідний потік. Математичний апарат теорії черг дозволяє аналізувати такі важливі характеристики системи, як середній час очікування в черзі, ймовірність відмови в обслуговуванні, коефіцієнт завантаження системи тощо [2, с. 82].
Одна з ключових переваг СМО полягає в їх здатності оптимізувати розподіл ресурсів. Наприклад, у контексті API-сервісів штучного інтелекту, де обчислювальні ресурси є обмеженими та дорогими, правильно спроектована система масового обслуговування може значно підвищити ефективність їх використання. Це досягається шляхом балансування навантаження між доступними серверами, пріоритизації запитів та динамічного масштабування ресурсів відповідно до поточного попиту [3].
Інша важлива перевага СМО - це їх здатність забезпечувати передбачувану якість обслуговування. Використовуючи математичні моделі, розробники можуть прогнозувати поведінку системи під різними навантаженнями та оптимізувати її параметри для досягнення бажаних показників продуктивності. Це особливо важливо для сервісів, які вимагають високої доступності та низької латентності, таких як системи авторизації або фінансові платформи.
Однак, системи масового обслуговування мають і свої обмеження. Одним з основних недоліків є складність їх точного моделювання в реальних умовах. Більшість математичних моделей СМО базуються на припущеннях про статистичні властивості вхідних потоків та часу обслуговування, які не завжди відповідають реальності. Це може призвести до розбіжностей між теоретичними прогнозами та фактичною поведінкою системи.
Інший виклик пов'язаний з балансуванням між ефективністю використання ресурсів та якістю обслуговування. Збільшення коефіцієнта завантаження системи може призвести до економії ресурсів, але також може збільшити час очікування в черзі та ймовірність відмов. Знаходження оптимального балансу вимагає ретельного аналізу та часто компромісних рішень.
У контексті сучасних тенденцій розвитку інформаційних технологій, системи масового обслуговування адаптуються до нових викликів. Зокрема, з розвитком мікросервісної архітектури та serverless-обчислень, традиційні моделі СМО еволюціонують, щоб враховувати динамічну природу цих середовищ. Наприклад, в serverless-архітектурі, де обчислювальні ресурси виділяються динамічно у відповідь на запити, моделі СМО повинні враховувати змінну кількість серверів та час їх "холодного" і "гарячого" старту.
Важливо відзначити роль сучасних інструментів у реалізації концепцій СМО. Наприклад, система обміну повідомленнями RabbitMQ часто використовується для створення розподілених систем, що реалізують принципи масового обслуговування. RabbitMQ дозволяє ефективно управляти чергами повідомлень, забезпечуючи надійну доставку та балансування навантаження між споживачами [4, с. 31].
Для ілюстрації важливості математичного апарату в моделюванні СМО, розглянемо кілька ключових формул. Наприклад, для системи М/М/1 (одноканальна система з пуассонівським вхідним потоком та експоненціальним розподілом часу обслуговування) середня довжина черги Lq визначається як:
де λ - інтенсивність вхідного потоку, а μ - інтенсивність обслуговування.
Середній час очікування в черзі Wq для такої системи можна обчислити за формулою:
Ці формули демонструють, як характеристики системи залежать від інтенсивності вхідного потоку та швидкості обслуговування, що є критично важливим для проектування ефективних API-сервісів та інших високонавантажених систем.
Дослідження в області СМО продовжують розвиватися, адаптуючись до нових технологічних парадигм. Зокрема, актуальними напрямками є розробка моделей для систем з гетерогенними ресурсами, врахування енергоефективності в оптимізації СМО, а також інтеграція методів машинного навчання для прогнозування навантаження та адаптивного управління ресурсами [5].
Підсумовуючи, можна сказати, що системи масового обслуговування залишаються невід'ємною частиною сучасної IT-інфраструктури, забезпечуючи теоретичну основу для проектування ефективних та надійних сервісів. Вони дозволяють знаходити оптимальний баланс між якістю обслуговування та ефективністю використання ресурсів, що є критичним для успіху в конкурентному середовищі цифрової економіки. Подальший розвиток теорії та практики СМО, особливо в контексті нових технологічних парадигм, залишається важливим напрямком досліджень та інновацій в області інформаційних технологій.
Список літератури
1. Li Y. Research on the queuing theory in practical applications. Applied and computational engineering. 2024. Vol. 54, no. 1. P. 41–47. URL: https://doi.org/10.54254/2755-2721/54/20241227.
2. Wang Y. Research on the queuing theory based on M/M/1 queuing model. Highlights in science, engineering and technology. 2023. Vol. 61. P. 80–87. URL: https://doi.org/10.54097/hset.v61i.10276.
3. Badmus E. Optimizing load balancing in queue-based systems: a small-world approach. 2024. URL: https://www.researchgate.net/publication/384116694_Optimizing_Load_Balancing_in_Queue-Based_Systems_A_Small-World_Approach.
4. Ćatović A., Buzađija N., Lemes S. Microservice development using RabbitMQ message broker. Science, engineering and technology. 2022. Vol. 2, no. 1. P. 30–37. URL: https://doi.org/10.54327/set2022/v2.i1.19.
5. Sherzer E. Can machines solve general queueing systems? 2022. URL: https://arxiv.org/abs/2202.01729.
|
Голосування 
Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License
Знайшли помилку? Виділіть помилковий текст мишкою і натисніть Ctrl + Enter