Infrared analyzers are now widely used for non-destructive testing of a large number of components made of composite materials in various industries [1]. Infrared thermography has emerged as a viable alternative to other more traditional non-destructive evaluation methods for testing a wide range of materials and structures. As a non-contact method, its ability to test large areas in short periods of time justifies a large amount of work and technical research. Interest in this technique has also been supported by the development of increasingly powerful equipment and data analysis tools in recent years.
The thermographic method typically involves applying heat to the part and using very sensitive infrared cameras to observe temperature transients on the surface of the sample [2, 3]. Anomalies in the part, such as voids, cavities or density changes, will change the temperature distribution and will be interpreted by the infrared camera as brighter or darker areas on the surface of the sample.
The traditional thermographic approach uses a pulsed heat source, and the spatial temperature response at different times after heating is used to detect defects. A key factor in all thermographic inspections is the diffusion mechanism that controls the transfer of heat through the part, and in this respect infrared thermography differs from conventional methods such as ultrasound, which are controlled by the wave propagation mechanism. This diffusion-controlled process presents interpretation challenges, since the solution of the transient thermal problem is very complex even for the simplest geometric and material cases.
Three main types of (optical) active thermography methods are commonly used: lock-in thermography, pulsed thermography and pulsed phase thermography. Continuous injection of low-frequency sinusoidal thermal waves into the sample is typical for lock-in thermography [4]. Monitoring the incident and reflected thermal waves over a period of time allows detection of subsurface voids. This technique relies on the results of amplitude attenuation and phase shift.
Discrete Fourier transform is used to extract frequency information from pulsed phase thermography data. For a given sampling rate (fs = 1/∆t), the total number of images N dictates the minimum available frequency (fmin = fs/N). The maximum available frequency is given by half the sampling rate (fmax = fs/2), since nmax = N/2, i.e. the Nyquist frequency fc. In order for low-frequency components to penetrate deeper below the surface, it is necessary to use a large ∆t or a large N.
The wavelet transform (with complex wavelets providing amplitude and phase information) can be used with pulsed phase thermography data in a similar way to the Fourier transform, but with the advantage of preserving the temporal information of the signal, which can then be related to the depth of the defect, thus allowing quantitative assessment. The infrared thermography model proposed in this paper assumed the use of the Morlet wavelet, namely a complex sinusoid in a Gaussian envelope, where the central frequency fc determines the number of significant oscillations of the complex sinusoid in a Gaussian window. The sinusoidal characteristic and excellent linear phase property make the complex Morlet wavelet an ideal candidate for the analysis of pulsed phase thermography.
Thermal simulation data were used to analyze the theoretical properties of thermal contrast signals. Circular defects (d = 16 mm) in carbon fiber reinforced plastic at different defect depths were simulated (with relative anisotropic thermal conductivity and density kx = 1.28, kz = 0.64, C = 1200, p = 1600, axially symmetric simulation). The simulation result was formed as a matrix of the time evolution of the temperature surface line profile (L =100 mm) after pulse excitation. The line profile was "placed" above the defect. The simulation was limited to N = 1024 samples with a sampling frequency fs of 25 Hz, which implies a minimum frequency of 0.024 Hz. The analysis of the amplitude spectra of the thermal contrast signals at different defect depths (from 1 mm to 5.5 mm with a step of 0.5 mm) indicates that most of the signal energy is concentrated in the frequency components below about 0.1 Hz.
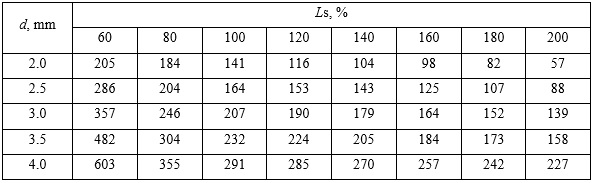
The results of the phase correlation for the translation parameter Δ depending on the depth d of the defects in composite samples with a relative characteristic size Ls are shown in Table 1.
Table 1. Phase correlation for the translation parameter Δ
In addition, the simulation results indicate that the position of the maximum of the thermographic phase contrast depends linearly on the depth d of the defect.
References:
1. Gupta R. et al. A review of sensing technologies for non-destructive evaluation of structural composite materials. Journal of Composite Science. 2012. Vol. 5(12). P. 319. https://doi.org/ 10.3390/jcs5120319
2. Olafsson G. et al. Lock-in thermography using miniature infra-red cameras and integrated actuators for defect identification in composite materials. Optics&Laser Technology. 2022. Vol. 147. P. 107629. https://doi.org/10.1016/j.optlastec.2021.107629
3. Aldave I.J. et al. Review of thermal imaging systems in composite defect detection. Infrared Physics&Technology. 2013. Vol. 61. Pp. 167-175. https://doi.org/10.1016/j.infrared.2013.07.009
4. Pitaressi G. Lock-in signal post-processing techniques in infra-red thermography for materials structural evolution. Experimental Mechanics. 2015. Vol. 55. Pp. 667-680. https://doi.org/10.1007/s11340-013-9827-1
|
Голосування 
Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License
Знайшли помилку? Виділіть помилковий текст мишкою і натисніть Ctrl + Enter