Вступ
Визначення хвильового фронту випромінення, яке виходить з оптичних систем, є критично важливим для забезпечення високої точності та якості зображень у різних оптичних приладах. Одним із найпоширеніших методів вимірювання хвильового фронту є використання сенсора Гартмана-Шека [1], який дозволяє отримувати детальну інформацію про аберації оптичної системи шляхом аналізу відхилень софкусованих світлових променів. Пірамідальний сенсор [2] також використовується для визначення хвильового фронту, забезпечуючи високу роздільну здатність та чутливість до фазових змін. Використання методів визначення хвильового фронту є ключовим для оптимізації оптичних систем, що застосовуються в астрономії, мікроскопії та інших високоточних наукових дослідженнях. Втім, застосування спеціалізованих сенсорів та інших додаткових оптичних елементів може також призвести до спотворень вимірювань через неідеальність обладнання, що призводить до необхідності додаткових розрахунків для компенсування [3] та уточнення. За таких обмежень, актуальним напрямком досліджень стає пошук рішень зі спрощеною оптичною складовою для приладів вимірювання хвильового фронту. Через стрімкий розвиток методів штучного інтелекту, все частіше пропонується використовувати методи на основі одного з найбільш популярних його видів – штучних нейронних мереж.
Аналіз літературних джерел
Огляд методів для вимірювання хвильового фронту із застосуванням нейронних мереж наведено в роботі [4]. За наведеними раніше причинами, відмова від застосування спеціалізованих сенсорів є особливо актуальною в тому числі для малогабаритних оптичних пристроїв, а також пристроїв, для яких необхідна швидка компенсація аберацій в реальному часі. Це призвело до появи класу методів визначення хвильового фронту на основі зображення (англ. image-based). Наприклад, в роботі [5] запропоновано використовувати згорткову нейронну мережу для визначення аберацій шляхом аналізу зображення інтенсивності світла від підсвічування досліджуваної оптичної системи точковим джерелом світла. Основним компонентом обробки даних виступає адаптована для задач регресії згорткова мережа для класифікації зображень Xception [6]. Отримані результати дають можливість стверджувати, що використання такого підходу є релевантним та таким, що дозволяє вимірювати хвильовий фронт доволі точно лише за інформацією з одного детектора. Однак застосування згорткових мереж високої ємності та точності призводить до необхідності використання більш продуктивного, і, як наслідок, дорожчого обладнання, що прямо впливає на можливість інтеграції подібних рішень в оптико-електронні прилади. Таким чином, постає необхідність розробки більш ефективних способів визначення хвильового фронту на основі зображення з детектора.
Запропоноване рішення
В даній роботі пропонується подолати необхідність використання двовимірних згорткових шарів шляхом представлення даних на детекторі у вигляді одновимірної сигнатури світлової плями, що утворюється після проходження через досліджувану оптичну систему. Сигнатура являє собою два вектори, що складаються з координат пікселів (X та Y) на детекторі, що обрамляють світлову пляму, яку можна отримати шляхом фільтрації та порогової обробки двовимірного зображення інтенсивності падаючого світла. Саме таке представлення сигнатури, а не у вигляді Фур’є-розкладу [7], обумовлено двома причинами. По-перше, це значно спрощує процес підготовки зображення перед обробкою нейронною мережею. По-друге, через потенційно велику абсолютну різницю між амплітудами гармонік, постає потреба у пошуку способу нормалізації вхідних значень для нейронної мережі з метою покращення стабільності навчання.
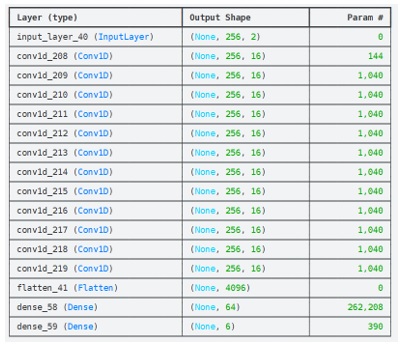
Запропонована нейронна мережа складається з одновимірних згорткових та повнозв’язних шарів, які використовують функції активації ELU [8] та tanh відповідно (Рис.1).
Рис.1. – Запропонована нейронна мережа, підготовлена в середовищі Kaggle [9].
Вхідними даними для мережі є 2 вектори, що містять в собі координати по осях Х та Y сигнатури світлової плями, а вихідними – коефіцієнти Церніке, що описують хвильовий фронт випромінення. Очевидно, що сигнатура світлової плями може містити різну кількість пікселів за різних аберацій та роздільної здатності детектора, тому вхідний вектор завжди приводиться до фіксованої довжини шляхом застосування інтерполяції. Вихідні значення коефіцієнтів Церніке є нормованими до [0; 1].
Результати
Працездатність рішення перевірено шляхом імплементації та навчання нейронної мережі на мові програмування Python в середовищі Kaggle [9] із застосуванням бібліотек TensorFlow [10], Scipy [11], Matplolib [12]. Навчаючу та тестувальну вибірки згенеровано за допомогою підготовленого в середовищі MATLAB [13] скрипту для спрощеного віртуального рейтресингу, який генерує зображення на детекторі, який знаходиться на відстані 65 мм від апертури діаметром 6 мм. Розмір навчаючої вибірки становить 9000 наборів сигнатур та відповідних їм наборів коефіцієнтів Церніке, тестова вибірка – 1000 наборів. Довжина сигнатури – 256 точок, згенерований хвильовий фронт описують 7 мод найменшого порядку (за виключенням першої моди, яка не змінює сигнатуру). Для навчання обрано оптимізатор Adam [14] з початковим коефіцієнтом навчання 0.0001, який поступово зменшується після навчання кожної міні-вибірки розміром у 32 примірники. Тривалість навчання – 100 епох. В якості функції втрат обрано середньоквадратичну похибку. Динаміку зміни її значення під час навчання та середню похибку для тестової вибірки наведено на Рис.2.
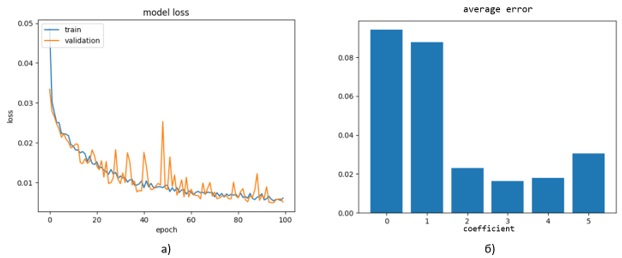
Рис.2. – Результати навчання та перевірки запропонованого рішення: а) зміна значень функції втрат для навчаючої та валідаційної вибірок; б) середня відносна похибка для тестової вибірки.
За результатами визначення коефіцієнтів Церніке для тестової вибірки, можна стверджувати, що запропоноване рішення є доволі точним – середня похибка не перевищує 10%, а для деяких коефіцієнтів – не більше 4% і може бути базовим для розробки більш досконалих методів визначення хвильового фронту за сигнатурою світлової плями.
Висновки
В даній роботі запропоновано та перевірено метод визначення хвильового фронту нейронною мережею за сигнатурою світлової плями. Середня похибка для 2-ї та 3-ї мод Церніке (перша не використовується в роботі) є меншою за 10%, а для 4-7 не перевищує 4%, що дає підстави стверджувати, що запропоноване рішення є працездатним. Таким чином, представлення вимірювання у вигляді сигнатури дозволяє збільшити ефективність роботи нейронної мережі (одновимірні згорткові шари розраховуються швидше за двовимірні), а отриманий результат є точним. Однак варто наголосити на тому, що запропоноване рішення не завжди може використовуватись для отримання остаточного результату через відсутність корекції оцінки коефіцієнтів в загальному алгоритмі роботи. Тому, очевидно, що напрямками подальших досліджень та вдосконалень мають бути: пошук кращих архітектур нейронних мереж, розробка нових або адаптація вже існуючих алгоритмів корекції кінцевого результату.
Список використаних джерел
1. Shack R.V., Smith F. Dow, “Production and use of a lenticular Hartmann screen”, Journal of the Optical Society of America”, 61 (5), 1971, Ramada Inn, Tucson, Arizona, 656., https://doi.org/10.1364/JOSA.61.000648
2. Ragazzoni R, “Pupil plane wavefront sensing with an oscillating prism”, Journal of Modern Optics, 43(2), 1996, pp. 289–293, https://doi.org/10.1080/09500349608232742
3. Deo V., Gendron E., Rousset G., Vidal F., Sevin A., Ferreira F., Gratadour D., and Buey T, “A telescope-ready approach for modal compensation of pyramid wavefront sensor optical gain”, Astronomy & Astrophysics, 629, 2019, A107, https://doi.org/10.1051/0004-6361/201935847
4. Alison P. Wong, Barnaby R. M. Norris, Deo Vincent, Guyon Olivier, Peter G. Tuthill, Lozi Julien, Vievard Sébastien, Ahn Kyohoon, “Machine learning for wavefront sensing”, Proc. SPIE 12185, Adaptive Optics Systems VIII, 121852I, 29 August 2022, https://doi.org/10.1117/12.2628869
5. Yohei Nishizaki, Matias Valdivia, Ryoichi Horisaki, Katsuhisa Kitaguchi, Mamoru Saito, Jun Tanida, and Esteban Vera, "Deep learning wavefront sensing," Opt. Express 27, 240-251 (2019)
6. F. Chollet, “Xception: Deep learning with depthwise separable convolutions,” in 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), (IEEE, 2017), pp. 1800–1807.
7. Yuan, Zhanwei & Li, Fuguo & Zhang, Peng & Chen, Bo. (2014). Description of shape characteristics through Fourier and wavelet analysis. Chinese Journal of Aeronautics. 27. 160–168. 10.1016/j.cja.2013.07.011.
8. Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). URL: https://arxiv.org/abs/1511.07289
9. Your machine learning and Data Science Community. Kaggle. URL: https://www.kaggle.com/
10. TensorFlow. URL: https://www.tensorflow.org/
11. A blue circle with a snake in the shape of the letter “S”. Scipy. URL: https://scipy.org/
12. Visualization with python. Matplotlib. URL: https://matplotlib.org/
13. MATLAB. MathWorks. URL: https://www.mathworks.com/products/matlab.html
14. D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” arXiv.org, 30-Jan-2017. URL: https://arxiv.org/abs/1412.6980.
_______________________
Науковий керівник: Яганов Петро Олексійович, кандидат технічних наук, доцент, Національний технічний університет України «Київський політехнічний інститут імені Ігоря Сікорського»
|