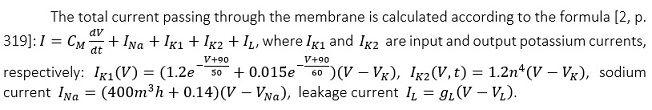Cardiovascular diseases are the most common cause of death in the world. Therefore, the relevance of studying the processes occurring in the heart is of importance for solving problems such as cardiac arrhythmias, cardiotoxicity of drugs and many others. One of the methods that is widely used in various fields of science, including for conducting research in medicine, is modeling. The advantage of this method is possibiliy to study the essential properties of object, based on the created model. Differential equations can be used to model complex biophysical and physiological processes occurring in the heart. Many mathematical models which take into account various physiological aspects of the heart have been developed.
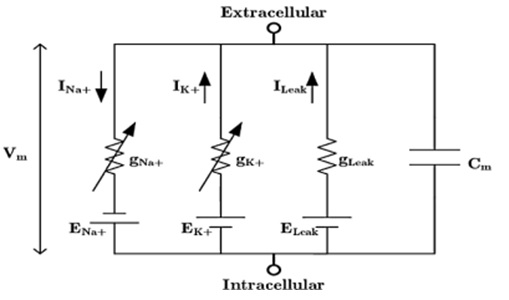
Most of the mathematical models for describing cardiac activity are modifications of the basic Hodgkin-Huxley model, which is a system of first-order nonlinear differential equations for describing the ionic mechanisms underlying the generation and propagation of action potentials in the squid giant axon. According to this model, the cell membrane is considered as a capacitor. The equivalent electrical circuit is depicted in Fig.1.
Fig.1. The equivalent electrical circuit of the cell membrane by Hodgkin-Huxley model
The value of the total current through the membrane consists of two components, namely the value of the capacitive current and the value of the ion current [1, p. 504]
Despite its effectiveness for describing processes occurring in neurons, the Hodgkin-Huxley model doesn't quite fit for heart cells. Despite this, it became the basis for the creation of other more accurate models.
Based on electrophysiological data obtained in experiments on Purkinje fibers, Denis Noble adapted the Hodgkin-Huxley model for cardiomyocytes, creating a new model known as the Noble’s model, which is a system of four first-order differential equations. It takes into account the presence of additional ion currents, which makes it possible to study in detail the dynamics of the processes occurring during the generation of the action potential by the heart cells and its change under the influence of certain environmental factors.
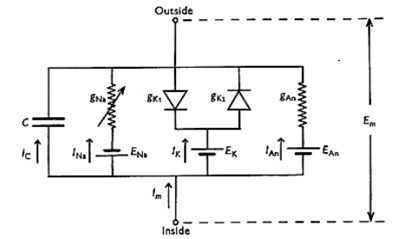
In Noble's model, the equivalent electrical circuit of the membrane of Purkinje fibers has the form [2, p. 320]:
Fig.1. The equivalent electrical circuit of the cell membrane by Noble’s model
The main difference of this model is that it assumes the presence of two types of potassium channels. The input potassium current (IK1) passes through the first type and the output current (IK2) through the second type. There is the absence of an external current in the model, because heart cells do not need external stimulation [3, p. 77].
It should be noted that all coefficients in the model are obtained on the basis of many experiments conducted on Purkinje fibers. In particular, the coefficients 400 and 0.14 in the formula for determining the sodium current are related to the fact that the resting membrane potential of heart cells is much lower, compared to neurons. So, much larger charge of sodium ions is required to generate an action potential.
Conclusion. In this work, it was shown that the physiological processes occurring in the heart can be studied by modeling using differential equations. In particular, the use of the Hodgkin-Huxley and Noble’s models to study the dynamics of the processes that occur during the generation and propagation of the action potential by cardiomyocytes is shown.
References:
1. Hodgkin A., Huxley A. A quantitative description of membrane current and its application to conduction and excitation in nerve. Journal of Physiology, 1952, vol. 117, no. 4, pp. 500-544.
2. Noble D. A modification of the Hodgkin-Huxley equation applicable to Purkinje fibers action and pace-maker potentials. Journal of Physiology, 1962, vol. 160, pp. 317-352.
3. Kostyuk P.G., Zyma V.L., Magura І.S., Miroshnychenko М.S., Shuba М.F. Biophysics / Edited by P. G. Kostyuk. - K.: Oberegy, 2001. – 544 p.
|
Голосування 
Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License
Знайшли помилку? Виділіть помилковий текст мишкою і натисніть Ctrl + Enter