Ключові слова: Ель-Ніньо, SINDy, диференціальні рівняння із запізненням, нелінійна динаміка.
Анотація: В цій роботі було розглянуто задачу реконструювання динаміки системи диференціальних рівнянь із запізненням (DDE), використовуя метод Sparse Identification of Nonlinear Dynamics (SINDy). У якості модельної системи розглянуто рівняння Ель-Ніньо [1]. Метод SINDy дозволяє ідентифікувати ключові нелінійні взаємодії у системі, що може бути важливо для прогнозування та керування кліматичними змінами [2].
В основі дослідження лежить реалізація часового ряду моделі Ель-Ніньо, що використовує диференціальні рівняння із запізненням для відтворення динаміки системи у вигляді
y'(t)=y(t)-y3 (t)-αy(t-τ). (1)
Параметри для моделі (1) були встановлені наступним чином: α= 0.75, затримка τ=7. Часовий інтервал моделювання визначено як від 0 до 200 одиниць часу. Для розрахунків використовувався чисельний метод dde23 з опціями високої точності. Початкові значення визначались для відрізку [-τ,0]=1.
Після отримання часового ряду y(t), що надано на рис. 1.1, було виконано дослідження та обрахування параметру вкладення m та значення параметра затримки Такенсу tay. Потрібно відмітити, що визначення того що данні часового ряду є даними процесу із запізненням є нетривіальним завданням, але у цієї роботі це нам відомо.
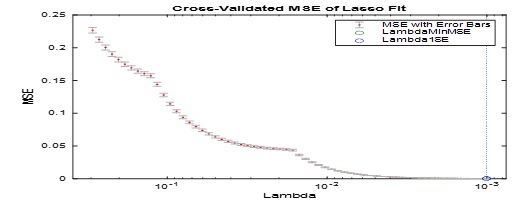
Результати моделювання були інтерпольовані для створення базісного набору даних, що після обробки методом SINDy дозволило ідентифікувати найбільш значущі терміни базису, що описують динаміку системи [3]. Для цього було використано L1 регресію (Lasso) із регуляризаційним параметром lambda = 1.0e-07.
Результати розрахунків програми виконувалось у середові Matlab та надано на рис. 1.1-1.4:
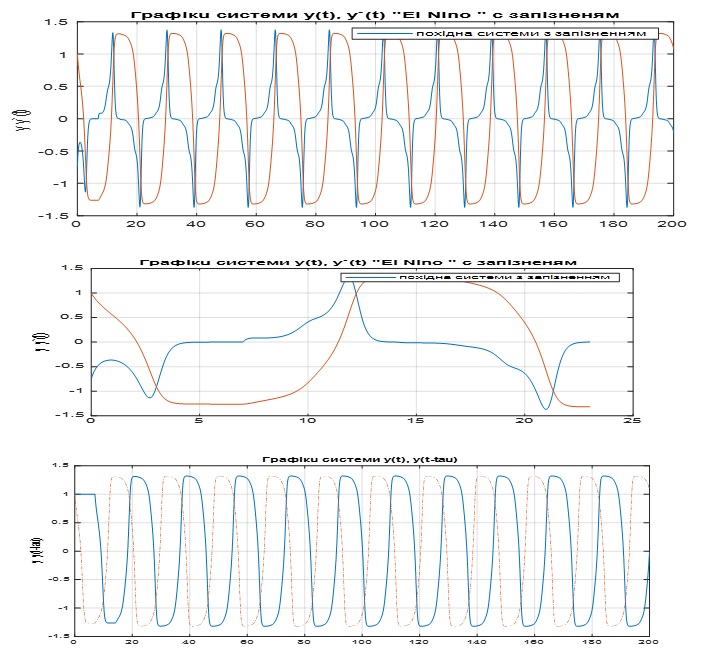
Рисунок 1.1 Графіки поведінки станів системи (1)
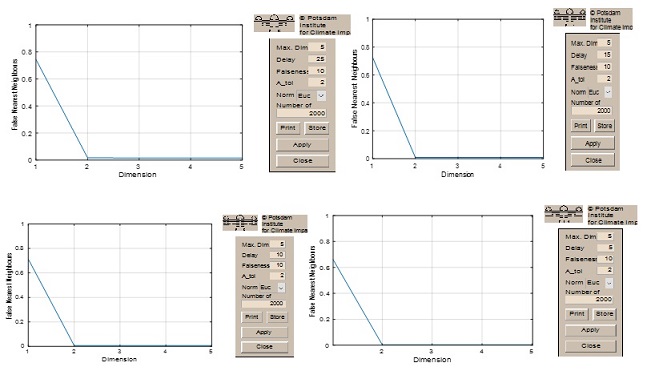
Рис. 1.2. Розрахунки значень параметру вкладення m для різних значень delay
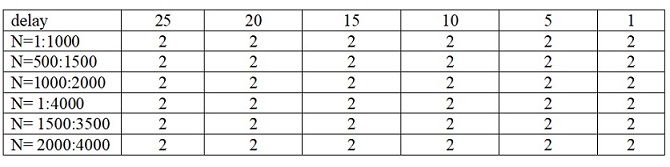
Обрахунки зроблено для наступних значень параметрів кількості точок у часовому ряді та значень параметру delay у табл.1. Табл.1
Розрахунок значення параметру вкладення m=2, але розмірність досліджуємої системи має m=1, тому що це рівняння має запізнення. Тому його потрібно більш детально дослідити на малому та більшому часовому проміжку та і N: 2000-4000 що надано у табл.1
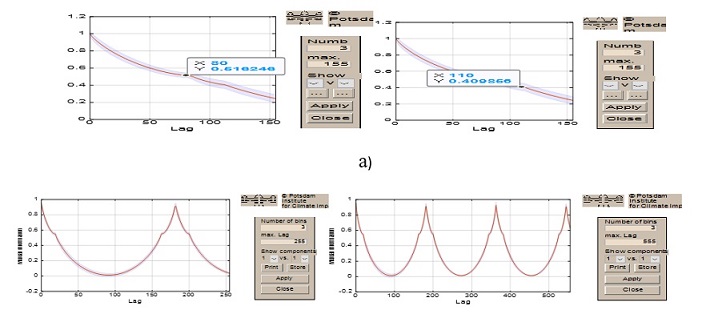
Розрахунок значень параметра затримки Такєнсу τ – це перші мінімуми наступної кривої лінії, представлено на рис.1.3.
Рисунок 1.3. Визначення значень параметру Такєнсу a) N=2000, Т=23;b) щодо N=4000, T=200.
На наступному етапі будувался базис модельної системи (1) за методу SINDy. У якості базісних елементів системи було запропановано використати наступні стани та значення коєфіцієнтів елементів базису як кубічних поліномів, яки наведені у табл.2, останній стовбец (модельні данні).
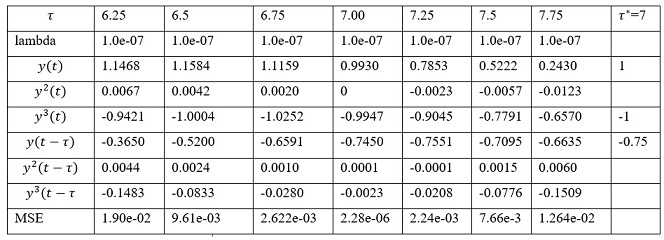
Табл.2. Отримані значення параметрів методу SINDy для наданих значень τ
Чисельні результати отримані за допомогою методу SINDy, який використовує L1 регуляризацію для виявлення найважливіших термів у моделі (1) надані у табл. 2. Графік виявлення значень параметру запізнення розраховувався з проміжку τ ϵ [6, 8] з деякім кроком, див. на Рис.1.4. Аналіз зміни MSE надано на рис. 1.5 для вказаних параметрів системи (1).
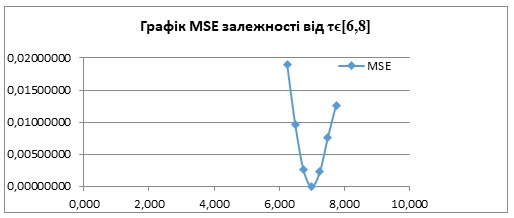
Рис. 1.4. Візуалізація помилки реконстукції коефіціентів системи (1) у залежності від параметра запізнення
Рис. 1.5. Графік розраховано щодо отриманих значень параметрів моделі (1): 0.9930, -0.9947 та -0.7450, значення lambda=1.0е-07.
Результати: Аналіз отриманих результатів показав, що використання методу SINDy дозволяє ідентифікувати ключові нелінійні процеси в системі El Niño. Нелінійні взаємодії та затримка впливають на поведінку системи, що важливо для розуміння механізмів її роботи. Візуалізація результатів підкреслює здатність, запропонованого алгоритму реалізації методу SINDy відновлювати складні динамічні структури, базуючись лише на обмеженій кількості спостережень.
Висновки: Метод SINDy, у наведенному використанні, демонструє можливість виявлення ключових динамічних закономірностей в системах що мають запізнення, що може сприяти кращому розумінню моделювання таких систем та прогнозуванню їх поведінки.
Список літератури:
1. Suarez M. J. and Schopf P. S. A delayed action oscillator for ENSO. J. Atmos. Sci. 1988. V. 45. P. 3283–3287.
2. Brunton S. L., Proctor J. L. and Kutz J. N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA. 2016. Vol. 113. No.15. P. 3932–3937.
3. SINDy for delay-differential equations: application to model bacterial zinc response/ Sandoz F., Ducret V., Gottwald A.G., Vilmart G., Perron K. December 14, 2022, P.1-21. URL: https://doi.org/10.1098/rspa.2022.0556.
|
Голосування 
Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License
Знайшли помилку? Виділіть помилковий текст мишкою і натисніть Ctrl + Enter