The fairly widespread use of polymer composites has led to the need to develop suitable methods and means of structural diagnostics applicable to two-component composite materials. Recently, the requirements for the technical condition of structural elements made of composite materials in a wide variety of industries have been increasing; diagnostic methods [1] must meet a number of conditions: they must be sensitive to various types of damage that occur in fiber composites and must provide damage detection [2], possibly at an early stage of their distribution and, finally, allow testing under environmental conditions [3, 4] and be inexpensivehe.
In this work, to analyze acoustic impulses in two-component composites, a continuous wavelet transform is used, which is based on square-integrable functions L2(R) in Hilbert space. Let us consider the propagation of wave group velocity pulses. The transit times of samples made of composite materials, determined by the wavelet transform method, are related to group velocities. In general, the deformations at different points in response to a broadband load consist of a range of frequencies, so it can be assumed that the wave propagates in an arbitrary direction with an exponential decay in time.
The basic acoustic wave is characterized by frequency ωС, phase velocity ωС/kС and modulation cos (∆kx − ∆ωt) with frequency ∆ω and propagation speed ∆ω/∆k. This wave can be described as a sequence of moving pulses (or groups, or wave packets). The phase and group velocities are denoted cP and cg, respectively.
The relationships between these velocities correspond to the following situations: A) cg > cP: wavelets appear in front of the group and disappear at the end of the group; B) cg < cP: wavelets accumulate at the end of the group, move through the group and disappear at the beginning. The results obtained for samples made of two-component composite material are shown in Tables 1 - 3.
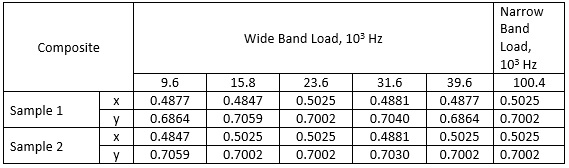
Table 1. Spatial distribution of applied load for composite plates
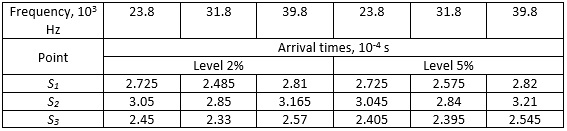
Table 2. Spectral distribution of arrival time of noisy signals (composite type 1)
Table 3. Spectral distribution of arrival time of noisy signals (composite type 2)
Numerical values indicate a decrease in arrival time with increasing frequency due to an increase in group velocities. Moreover, the results are in good agreement with the actual location of the applied load in the case of an anisotropic plate. Note that the error in estimating the coordinates of the load location is less than 1.2% for all different types of loading of both isotropic and anisotropic samples.
It should be noted that the processed sensor signals can differ significantly from the numerical simulation signals, and this is due to the fact that the data is often distorted by measurement noise. Let us consider the influence of noise on the results of wavelet analysis of the localization of the deformation field in the composite. An analytical consideration of the influence of noise on the results of the passage of an acoustic wave inside the volume of a composite can be represented as the sum of the original and noisy signals.
By adding a certain percentage of white noise to the system and denoising the signal using the usual moving average method, the described method can be used to determine the location of the effect. The results were tested for different noise levels (2% and 5%).
References:
1. Su Zh., Ye L., and Bu X. A damage identification technique for CFEP composite laminates using distributed piezoelectric transducers. Composite Structures. 2002. Vol. 57. Pp. 465-471. https://doi.org/10.1016/S0263-8223(02)00115-0
2. Zhou J., Li Z., and Chen J. Damage identification method based on continuous wavelet transform and mode shapes for composite laminates with cutouts. Composite Structures. 2018. Vol. 191. Pp. 12-23. https://doi.org/10.1016/j.compstruct.2018.02.028
3. Spagnoli A., Montanari L., Basu B., and Broderick B. Nonlinear damage identification in fiber-reinforced cracked composite beams through time-space wavelet analysis. Procedia Material Science. 2014. Vol. 3. Pp. 1579-1584. https://doi.org/10.1016/j.mspro.2014.06.255
4. Yan Y.J., Yam L.H. Online detector of crack damage in composite plates using embedded piezoelectric actuator sensors and wavelet analysis. Composite Structures. 2002. Vol. 58. Pp. 29-38. https://doi.org/10.1016/S0263-8223(02)0004-0
|
Голосування 
Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License
Знайшли помилку? Виділіть помилковий текст мишкою і натисніть Ctrl + Enter