The development of mineral extraction is impossible without the search for new solutions to applied problems related to a creation of effective technologies for the development of mineral deposits. The possibility of fundamental research in this field is enhanced by the involvement in the development of deposits with сomplex mining and geological conditions, particularly the fracturing of the enclosing rocks, as well as tectonic breakings in the massif.
Thіs paper describes the method of modeling a rock massif weakened by two systems of cracks. The first of them is the so-called geological discontinuity (breaking), the second is small endogenous cracks, located between the breakings. Geological breakings are presented as a few large, evenly spaced cracks with parallel breaked planes, the stiffness of which is rather high. The rock between geological breakings is weakened by endogenous fracturing. This is another type of crack, smaller, less rigid. Their presence leads to a weakening of the rock’s physical and mechanical properties in the direction perpendicular to the crack direction.
Modeling of such a massif was performed by combining two methods. Rocks weakened by endogenous fracturing are considered as an anisotropic material in which the plane of transverse anisotropy is parallel to the crack planes [1]. In the direction perpendicular to this plane, the elastic properties are weakened [2]. For the geological breakings modelling the modification of the boundary element method – the method of discontinuous displacements – is used [3].
The numerical procedure for implementing the boundary element method for a medium weakened by two systems of cracks combines both approaches [4].
With the help of the described method, a numerical solution of the problem of determining the stress-strain state around the cavity in the massif, weakened by endogenous cracking along the layering, which contains a geological breaking, the plane of which is located across the layering, was obtained.
The cavity of a rectangular cross-section 1m x 4m is located at the depth of 800 m in the coal seam with the inclination angle α. Characteristics of the undisturbed massif: enclosing rocks density γ=2,5·103kg/m3, Young's modulus E0=3,5·104kg/sm2, Poison’s ratio v=0,17, compressive strength limit σc=220 kg/sm2. Endogenous cracks are located at a distance 20sm from each other. Young's modulus in the direction perpendicular to the cracks is E1=0,1E0. The plane of the geological breaking is located perpendicular to the seam at a distance d from the working contour.
The obtained results make it possible to estimate the geological breaking influence on the stress-strain state of the described massif area. In the case of a flat seam (α=0o), the geological rupture relieves the cavity from the lateral pressure of rocks. At the same time, stresses exceeding the permissible ones are concentrated on the rupture itself and spread to its surroundings. When the distance between the rupture and the cavity is reduced to two meters, the region of stresses, which exceed the permissible limits, captures the edge of the cavity. If the rupture is located at a distance of more than three meters, it restrains the pressure of the side rocks, and at a distance of six meters, it practically ceases to affect on the stresses distribution around the
cavity, somewhat reducing their level.
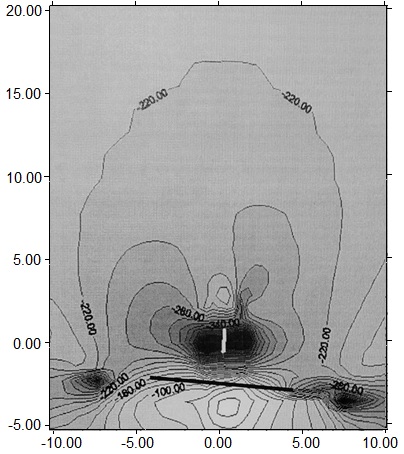
When the seam is steeply dipping (α=85o), the presence of the rupture significantly worsens the stress state, increasing the pressure from below. Thus, the presence of a geological rupture 8 m long, located at the distance of 2 m from the lower (lying) edge of the cavity, creates a large area of stresses that exceed the permissible ones. It captures the entire cavity and spreads to a height of 18 m above the top (overhanging) edge of the cavity. Thus, a geological rupture located under the lying edge of the cavity in a steeply dipping layer leads to a loss of rock stability in a large area of the massif. Only at more than 10 m from the cavity, the influence of the geological rupture weakens and gradually disappears. Figure 1 shows the stress contours for a steeply dipping seam; distances – in meters, stresses – in kg/sm2.
Fig. 1. Stress distribution around the cavity in the rock massif with endogenous fracturing and geological rupture.
REFERENCES
1. Prykhodko V.V. Modeling of stress-strain state of fractured rock mass nearby of conjugated workings / V.V. Prykhodko, N.P. Ulanova // Naukovyi Visnyk Natsionalnoho Hirnychoho Universytetu, 1, 2018. – pp. 5–12.
2. Goodman R.E. Methods of geological engineering. – St. Paul : West, 1976.
3. Rizzo F.J., Shippy D.J. A formulation and solution procedure for the general nonhomogeneous elastic inclusion problem // Int. J. Solids and Structures, 1968, 10. – pp. 1161-1179.
4. Kuzmenko A.M. Rock Mass with Two Systems of Cracks Model / A.M. Kuzmenko, V.V. Prykhodko, N.P. Ulanova, V.I. Dotsenko // Geotechnological Issues of Underground Space Use for Invironmentally Protected World, 2001. – рp. 97-100.
|
Голосування 
Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License
Знайшли помилку? Виділіть помилковий текст мишкою і натисніть Ctrl + Enter