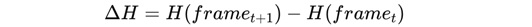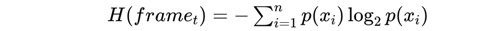Cryptographic systems are essential for ensuring the confidentiality, integrity, and authenticity of digital communications. The need for robust cryptographic security systems is more critical than ever, particularly with the increasing risks of cyber threats and the advent of quantum computing potentially compromising traditional encryption methods [1]. The strength of these systems largely depends on the unpredictability of their random number generators (RNGs) [2].
Traditional random number generators (RNGs) often rely on algorithmic methods which, while efficient, suffer from predictability and potential vulnerabilities to reverse engineering attacks [1, 3]. Current hardware RNGs that use quantum phenomena or thermal noise are secure but can be prohibitively expensive and complex for widespread application [3]. Studies indicate that web cameras, ubiquitous and inexpensive, can capture inherent stochastic processes in their imagery due to light and sensor noise, offering a cost-effective alternative for generating entropy [4].
Current implementations of random number generation utilizing webcams predominantly rely on single-frame analysis as the input for the RNG. Given that the camera remains static, there is minimal variation from one frame to the next, which may not effectively mitigate biases and correlations [4]. These limitations can potentially compromise the security of the RNG's output [4]. Consequently, focusing research on enhancing the unpredictability of RNG outputs by reducing their dependence on static input images represents a promising direction for advancing the field.
The objective of the thesis is to propose a modification to existing random number generators (RNGs) that reduces their reliance on the initial images captured by web cameras, thereby minimizing biases and correlations between frames.
This thesis proposes enhancing the cryptographic applications of RNGs using a method that exploits the inter-frame chaos correlation captured by webcams. This involves analyzing changes in pixel intensity across consecutive frames to generate random numbers.
The proposed RNG method would capture video at high frame rates and compute the entropy based on the difference in pixel values between consecutive frames. The randomness extraction is quantified using the entropy difference formula [5]:
where H (framet) is the Shannon entropy for a frame at time t, calculated as [5]:
here, p (xi) is the probability of each pixel value xi.
Such a method should significantly amplify the sensitivity to minor variations in pixel values, attributable to the inherent noise and environmental changes, thereby enhancing the randomness quality.
This involves just a single additional operation with a time complexity of O(1).
Conclusions. To eliminate biases, it is suggested to utilize not the frame itself but the difference in pixel intensity between two consecutive frames. Incorporating this operation into the RNG algorithm involves a complexity of O(1), which does not significantly increase processing time. This maintains the simplicity and cost-effectiveness of using web cameras as a source for RNG. Additionally, the specific scene captured by the camera would no longer influence the RNG output, thereby enhancing its unpredictability and safeguarding against reverse engineering.
Subsequently, calculations using an actual camera should be performed. The randomness of the sequences generated can be evaluated using standard statistical tests for randomness, such as the NIST suite [4], to verify their compliance with cryptographic standards. The outcomes should then be compared to those from a general RNG that does not incorporate cross-frame calculations.
References:
1. Thomas Lugrin, Valentin Mulder, Alain Mermoud, "Random Number Generator", Trends in Data Protection and Encryption Technologies, Cham: Springer Nature Switzerland, pp. 31–34, 2023, doi:10.1007/978-3-031-33386-6_7, ISBN 978-3-031-33386-6.
2. National Institute of Standards and Technology (NIST), “Recommendation for the Entropy Sources Used for Random Bit Generation”, SP 800-90C, August 2022, https://doi.org/10.6028/NIST.SP.800-90C.
3. Seongmo Park, Byoung Gun Choi, Taewook Kang, Kyunghwan Park, Youngsu Kwon, Jongbum Kim, “Efficient hardware implementation and analysis of true random-number generator based on beta source.” ETRI Volume 42, Issue4, Special Issue on SoC and AI processors, pp 518-526, 2020, https://onlinelibrary.wiley.com/doi/full/10.4218/etrij.2020-0083.
4. Rigan Ap-apid, “Using a PC Camera to Generate Cryptographically Strong Random Numbers.”, Conference: Proceedings of the 2008 International Conference on Security & Management, 2008, 22-27, https://www.researchgate.net/publication/221199634_Using_a_PC_Camera_to_Generate_ Cryptographically_Strong_Random_Numbers
5. Information Technology Laboratory National Institute of Standards and Technology Gaithersburg, “SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions”, August 2015, http://dx.doi.org/10.6028/NIST.FIPS.202.
|
Голосування 
Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License
Знайшли помилку? Виділіть помилковий текст мишкою і натисніть Ctrl + Enter