Серед задач теорії розкладів, як з теоретичного, так і з практичного погляду, актуальною є задача оптимального планування скінченої множини подій, які повинні відбуватись в задані проміжки часу та мають циклічну структуру.
Однією з практичних сфер, де виникають такі задачі, є планування роботи громадського транспорту. Це нетривіальна задача, оскільки доводиться враховувати не лише очевидні обмеження, що випливають з постановки, а й ті, які здаються несуттєвими, але можуть впливати на оптимальність розв’язків.
Формалізація таких задач з використанням апарату теорії графів дозволяє представляти їх більш наглядно і розробляти ефективні підходи до пошуку розв’язків. У [1] така формалізація застосована для розв’язання задачі пов’язаної з оптимальним регулюванням роботи транспорту.
Розглядається задача, що формулюється наступним чином:
Нехай n – кількість подій, які необхідно упорядкувати на часовому проміжку T. Введемо множину V, де vᵢ ∈ [0, T) – час виникнення події i ∈ {1, ..., n}. Для деяких пар подій (i, j) відомі обмеження Lᵢⱼ, Aᵢⱼ ∈ Z, які є нижньою та верхньою межею часу між виникненням цих подій. Нехай U ⊆ V × V – пари подій, для яких існують обмеження. Тобто для кожної пари подій (i, j) ∈ U існує відрізок [Lᵢⱼ; Aᵢⱼ] і повинно виконуватися обмеження (vⱼ − vᵢ) mod T ∈ [Lᵢⱼ; Aᵢⱼ].
Необхідно по заданому орієнтовному графу G = (V, U) і відрізку [Lᵢⱼ; Aᵢⱼ], відомому для кожної пари подій (i, j) ∈ U (Lᵢⱼ, Aᵢⱼ ∈ Z+), та часовому періоду T знайти вектор v, такий що (vⱼ − vᵢ) mod T ∈ [Lᵢⱼ; Aᵢⱼ], ∀ (i, j) ∈ U, або встановити неможливість такого існування.
В [2] дана задача розглядається в контексті планування роботи залізничного транспорту, для якої пропонується новий евристичний підхід, основна ідея якого лежить у розбитті початкового графу на дерева, та розв’язання задачі з обмеженнями для них.
Оскільки розбиття графа на дерева може бути неоднозначним, то виникає питання – яке саме розбиття буде більш ефективним.
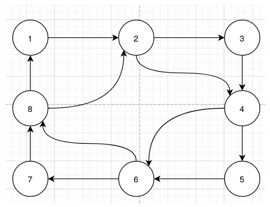
Продемонструємо, як різне розбиття графа на дерева впливає на швидкість знаходження розв’язку. Існує декілька варіантів розбиття фрагмента графа зображеного на рис. 1 на дерева.
Рисунок 1. Фрагмент графу
Одним з них є дерева 1 -> 2 -> 4 -> 6, 3, 5, 7 -> 8. При такому розбитті дерева пов’язані тільки з першим деревом, тобто не зв’язані між собою. Таким чином, достатньо знайти розв'язок задачі для першого дерева, який буде задовольняти обмеженням, що відповідають і іншим деревам. Це можливо, оскільки між ними відсутні зв’язки, наявність яких накладали б обмеження, що призведуть до збільшення ітерацій.
Розглянемо наступний варіант розбиття: 1 -> 2 -> 3, 4 -> 5, 6 -> 7, 8. У ньому суттєва залежність дерев одне від одного, а це означає, що при знаходженні розв’язку для першого дерева, що задовольнить обмеження з другого, обмеження з третього можуть бути не задовільнені. Це спричинить пошук нового розв’язку і призведе до збільшення часу.
В даній роботі пропонується нова схема розбиття графу на дерева, що лежить в основі наступного алгоритму:
1. Позначимо через k кількість дерев, на які розбивається граф.
2. k=1. Вважаємо всі вершини дерева непоміченими.
3. В графі G серед непомічених вершин обираємо вершину з найменшим ступенем, помічаємо її (орієнтація дуг не враховується) і вважаємо коренем k-го дерева (при рівності ступенів, вершина обирається довільно).
4. Якщо всі вершини помічені, то кінець – дерева побудовані.
5. Якщо серед непомічених вершин є вершини, які можна додати до поточного дерева, то послідовно обираємо вершини в порядку незростання їх ступенів, помічаємо їх, і додаємо до k-го дерева.
6. k:=k+1; G:=G; Перехід на крок 3.
Показано, що такий спосіб виділення дерев покращує значення цільової функції і не погіршує часові характеристики реалізації алгоритму знаходження розв’язків.
Список літератури:
1. Serafini P., Ukovich W. A. Periodic Job Shop Model. IFAC Proceedings Volumes. 1989. Vol. 22. Iss. 14. P. 89-94. URL: https://www.sciencedirect.com/science/article/pii/S1474667017543311 (11.04.2024)
2. Heuven van Staereling I. I. Scheduling Problems in the Service Industry: Theory and Applications. Amsterdam : Vrije Universiteit Amsterdam. 2023. 153 р. URL: https://ir.cwi.nl/pub/33353/33353D.pdf (03.04.2024)
|
Голосування 
Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License
Знайшли помилку? Виділіть помилковий текст мишкою і натисніть Ctrl + Enter