Розглядається математична задача побудови оптимальної стратегії інвестування у комерційному банку при урахуванні обмежень на обов’язкове резервування. Математична постановка задачі формулюється як задача нелінійного програмування з обмеженнями.
Прикладами таких математичних задач для реального сектору економіки можуть бути:
1. Задача про оптимальний розподіл інвестиційних ресурсів комерційного банку.
2. Задача про оптимальне кредитування комерційним банком.
3. Задача про оптимізацію розподілу активів комерційного банку з урахуванням обов’язкового резервування.
Формально задача про оптимальний розподіл інвестиційних ресурсів комерційного банку ідентична задачі інвестування у цінні папери на фондовому ринку, тому підходи, описані в [1], повністю або частково можна застосувати при розв’язанні задач п.1 та п.2.
При формальному математичному записі задачі п.3 звернемо увагу на те, що іноді більш зручно розглядати процеси інвестування не у частках капіталу, що виділяється для інвестування, а безпосередньо у сумі коштів, що виділяються для інвестування у тий напрямок. Задача матиме вигляд
де 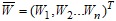 - вектор-стовпчик, координатами якого є суми коштів, що виділяються для інвестування у відповідні напрямки; r та p вектор-стовпчики розмірності n x 1, перший з яких характеризує очікувану прибутковість i - того інвестиційного напрямку, а другий - відсоток від суми, що може бути інвестована у відповідний напрямок і який є обов’язковим для резервування. Згідно Г. Марковицю, другий критерій класичної двокритеріальної задачі про оптимальний портфель інвестицій має вигляд
де σij - коваріація між i -тим та j -тим інвестиційними напрямками.
Векторно-матричний вигляд задачі є таким
де V - коваріаційна матриця; R - вектор розмірності n x 1, координатами якого є 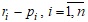 ; символ Т- знак транспонування. Маючи за мету побудувати аналітичний розв’язок задачі, і, виходячи із практичних міркувань, перший критерій в (1) замінимо рівністю ; символ Т- знак транспонування. Маючи за мету побудувати аналітичний розв’язок задачі, і, виходячи із практичних міркувань, перший критерій в (1) замінимо рівністю 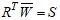 . .
Тоді (1) матиме вигляд нелінійної задачі одномірної оптимізації при обмеженнях
де S - бажаний рівень прибутку інвестиційної операції.
Застосуємо для її розв’язання метод множників Лагранжа. Функція Лагранжа
містить два невідомі параметри λ1 і λ2 і задача полягає у визначенні елементів вектора  . .
Параметри λ1 та λ2 визначимо із системи алгебраїчних рівнянь
Із першого рівняння
Із другого рівняння
Прирівняємо (3) та (4)
Розв’яжемо рівняння і знайдене значення параметра λ2 підставимо у (3) або (4) і визначимо λ1. Після підстановки визначених значень параметрів у (2) отримаємо шукані частки банківських інвестицій.
Для диверсифікації ризику портфеля часто банківські активи розподіляють не тільки серед ризикованих напрямків інвестування, але також і серед неризикованих [2]. Математична постановка задачі при цьому може бути такою
де W0- сума коштів, що виділяються на інвестування у неризиковані цінні папери. Як і для попередньої задачі, розглянемо однокритеріальну її постановку.
Функція Лагранжа
на відміну від попереднього випадку, містить додаткову невідому W0.
Для визначення невідомих параметрів λ1 та λ2 скористаємось другим та третім рівняннями системи (5). Після підстановки в них λ2 із (6) отримаємо лінійне алгебраїчне рівняння 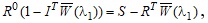 , ,
що містить невідому λ1. Розв’яжемо його і, підставивши λ1 у (6), визначимо λ2.
У даному науковому дослідженні сформульовано нові математичні постановки задач оптимізації алгоритмів прийняття інвестиційних рішень комерційним банком при наявності обмежень на резервування.
Список літератури:
1. Garashchenko F., Kulian V., Rutitskaya V. Modelling and Analysis of Investment Trends. // Journal of Automation and Information. –New York, Connecticut. -2011. –v. 43, issue 12, -P.48-58.
2. Zaychenko Y., Sydoruk I. Direct and dual problem of investment portfolio optimization under uncertainty. //International Journal “Information Technologies & Knowledge. – 2014. -v. 8, Number 3, -P.225-242.
|









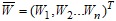 - вектор-стовпчик, координатами якого є суми коштів, що виділяються для інвестування у відповідні напрямки; r та p вектор-стовпчики розмірності n x 1, перший з яких характеризує очікувану прибутковість i - того інвестиційного напрямку, а другий - відсоток від суми, що може бути інвестована у відповідний напрямок і який є обов’язковим для резервування. Згідно Г. Марковицю, другий критерій класичної двокритеріальної задачі про оптимальний портфель інвестицій має вигляд
- вектор-стовпчик, координатами якого є суми коштів, що виділяються для інвестування у відповідні напрямки; r та p вектор-стовпчики розмірності n x 1, перший з яких характеризує очікувану прибутковість i - того інвестиційного напрямку, а другий - відсоток від суми, що може бути інвестована у відповідний напрямок і який є обов’язковим для резервування. Згідно Г. Марковицю, другий критерій класичної двокритеріальної задачі про оптимальний портфель інвестицій має вигляд 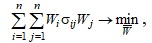

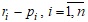 ; символ Т- знак транспонування. Маючи за мету побудувати аналітичний розв’язок задачі, і, виходячи із практичних міркувань, перший критерій в (1) замінимо рівністю
; символ Т- знак транспонування. Маючи за мету побудувати аналітичний розв’язок задачі, і, виходячи із практичних міркувань, перший критерій в (1) замінимо рівністю 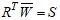 .
.
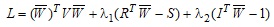
 .
. 








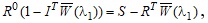 ,
,