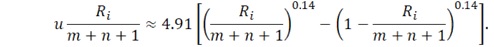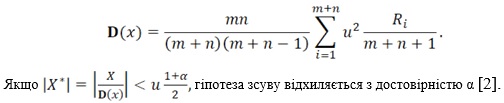Зважаючи на тенденцію феноменального прискорення нагромадження даних у сучасному світі, тема їх ефективного аналізу є надзвичайно актуальною. Виходячи з цього, правильний вибір методів статистичного аналізу є критично важливим для покращення роботи різних галузей (наприклад, медицина, машинобудування, неруйнівний контроль тощо), в яких будуть застосовані ці методи.
Метою роботи є розробка інформаційної технології, за допомогою якої проведено порівняння математичних очікувань при застосуванні параметричного та непараметричного критеріїв для різних за довжиною вибірок випадкових велечин. Наразі науковці, що досліджують статистичний аналіз дійшли висновку, що параметричні критерії є менш універсальними, але при цьому вони потужніші та ефективніші за непараметричні критерії [1]. Предметом дослідження є перевірка правильності даного твердження.
Параметричні критерії – це ті, які роблять припущення щодо параметрів розподілу випадкових величин, з яких складається вибірка. Це часто припущення про те, що дані розподілені за нормальним законом розподілу. Непараметричні критерії можуть використовуватися коли дані розподілені як за нормальним законом розподілу, так і за іншими (експоненціальними, логістичний, Релея, тощо).
Якщо використовувати непараметричні критерії в усіх випадках, то це б позбавило клопоту перевірки нормальності. Однак параметричним критеріям надають перевагу з наступних причин:
1. Часто потрібна не лише перевірка значущості; досліджується також і вибірка, з якої надійшли зразки, і це найкраще зробити з допомогою оцінки параметрів і довірчих інтервалів.
2. Важко виконувати гнучке моделювання за допомогою непараметричних тестів.
3. Параметричні тести зазвичай мають більшу статистичну потужність, ніж їхні непараметричні еквіваленти. Іншими словами, існує більша ймовірність виявити значні відмінності між вибірками, коли вони справді існують.
Вхідними параметрами у досліді будуть виступати вибірки розміром 10, 20 та 40; з логістичним та експоненціальним законами розподілу ймовірностей; з довірчим інтервалом із надійністю 0,95. У якості критеріїв для порівняння обрано: параметричний критерій Стьюдента та еквівалентний непараметричний критерій Ван дер Вардена.
Досліджуючи ці критерії у віртуальному середовищі MATLAB, для критерію Стьюдента використовується формула:
а для Ван дер Вардена наступна:
де u – γ-квантиль стандартного нормального розподілу.
Для обчислення квантилів 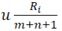 може бути застосовано наближення
Гіпотеза зсуву відхиляється, якщо ½C½< xa, де xa – критичне значення, наведене у спеціальній таблиці [2].
При n >=20 розподіл X задовільно описується нормальним із середнім μ=M(x)=0 та дисперсією
Виконуючи порівняння критеріїв отримуємо результати представлені в таблиці 1.
Таблиця 1
З отриманих даних можна зробити висновок, що при n→∞ ефективність критерію Ван дер Вардена не поступається ефективності критерію Стьюдента.
Виходячи з інформації про універсальність, потужність та ефективність різних типів критеріїв за певних умов та з різною довжиною вибірок, є змога краще застосовувати статистичний аналіз у різноманітних сферах: науках (від фізики до соціології), виробництва, техніки, соціально-економічної сфери тощо.
Список використаних джерел:
1. Методи аналізу даних : навчальний посібник для студентів / В.Є. Бахрушин. – Запоріжжя : КПУ, 2011. – 268 с.
2. Кобзарь А.И. Прикладная математическая статистика. – М.: ФИЗМАТЛИТ, 2006. – 816с.
|








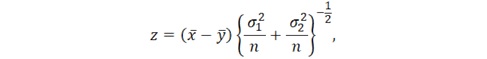

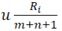 може бути застосовано наближення
може бути застосовано наближення